Nonlinear Dynamics, Systems Thinking
Adapted from the article originally written by Ernest Lemaiyan
for the Cabrera's Cornell University, System Thinking in Public Affairs Course
The field of non-linear dynamics is dedicated to study systems that exhibit behavior that cannot be described by equations of the ‘y = ax + b’ format [1], the field even covers problems that are deterministic or seem physically simple at first [2]. Starting with the naming of the field, the two keywords used are; dynamics and non-linear. Simply put ‘dynamics’ is the study of changes in a system with time. Next is the term ‘non-linear’, which is used as a description of certain types of systems encountered in mathematics and the sciences. In non-linear systems the relation between important variables is not proportional. Illustration can be done with the simple example of a bird feeding: a bird eats 2 grains a day, 2 birds eat 4, what would 3 birds consume? If the answer is 6 the system is linear of the form y=2x, however if it is 13 grains a day the bird-grain relation is non-linear.
Non- linear systems are described as not instinctively imaginable, as humans tend to think in roughly linear timescales and relations [3]. And this field is of interest to mathematicians, engineers and scientists because most of the mathematical descriptions of real-world systems can only be modelled by a nonlinear system of equations involving polynomials higher than one degree or by differential equations. A compendium of nonlinear dynamical systems, and the sub-groups involved, were tabulated in the works of the mathematician Steven Strogatz [10]. It is noticeable that all systems listed require higher lever mathematical skill to evaluate. This is because even in mathematics and the sciences, the importance of the non-linear systems is usually only stressed later. Usually, the foundational understanding is based on simplified classical models with assumptions of linearity [4].
The usage of non-linear system of equations is so ubiquitous that linear equations are an exception to the norm when applying mathematics to real-world systems [5]. This is because non-linear dynamics is used in modelling non-linear oscillators like heart movement in fibrillation, fluid behavior of vortices in air flow and complex mechanics such as the movement of paired blackholes.
A key sub-field in this area of non-linear dynamics is the study of chaos. Chaos theory was popularized by the unintuitive characterization of a butterfly flapping its wings and causing a hurricane elsewhere after some time. The imagery was used to capture an essential bit of chaos theory, that some systems show high sensitivity to initial conditions [6]. The other bit is that a characteristic structure is exhibited. To avoid a common misapprehension that follows, it must be stated that although the behavior is complex it is not random.
Non-Linear dynamical equations are difficult to solve so solutions are found via linearization [7], which is also limited in capturing other phenomena. Chaotic systems are even more difficult to solve analytically via pen and paper, and computers must be used.
To drive this point home, a historical case in point is useful. Newton by 1866 had used differential equations and his three newly invented laws to solve the 2-body problem wherein gravity is the explanation for elliptical orbits. However, when faced with the 3-body problem of adding to the sun and a single planet an extra body; a moon, proved to be too difficult. This was a case of a system that could exhibit chaotic behavior and none of the great mathematicians after Newton, whether Gauss or Euler could prove the orbits analytically. Only Poincare gave a geometric explanation as to why the analytic solution was not possible [8].
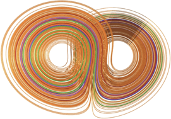
Figure: Colorful version of Lorentz attractor showing solutions of his 3 variable ODEs, also called Lorentz’s Butterfly. [6]
To recapitulate in conclusion, non-linear dynamics is a field steeped in applied mathematics and offers a gamut of versatile ‘real-world’ analysis tools. The unintuitive results of the subject and its various subfields such as the chaos theory, show that nature is delicate, multivariate and not easily compatible with our simple approximations. Just as John Haldane opined; Reality is not only stranger than we suppose, it is much stranger than we can suppose [9].
Bibliography:
[1] Springer Nature Publishing AG. “Non-Linear dynamics”. Nature.com. (2019). https://www.nature.com/subjects/nonlinear-dynamics
[2] R. Cuerno, A. F. Rañada, and J. J. Ruiz‐Lorenzo. Deterministic chaos in the elastic pendulum: A simple laboratory for nonlinear dynamics. American Journal of Physics Vol. 60. 73 (1992).
[3] B. Langhe, S. Puntoni and R. Larrick. Linear Thinking in a Nonlinear World. Harvard Business Review. May-June Issue (2017). Pp 130-139.
[4] A. Downey. “Chapter 1: Complexity Science”. In Think complexity: Complexity science and computational modeling. O’Reilly. (2018). Pp 2-4.
[5] Campbell, David K. (25 November 2004). "Nonlinear physics: Fresh breather". Nature. 432 (7016): 455–456
[6] McWilliams, J. C. (2019). A perspective on the legacy of Edward Lorenz. Earth and Space Science, 6, 336– 350. https://doi.org/10.1029/2018EA000434
[7] B. N. Pshenichnyi, A. A. Sosnovsky. The linearization method: Principal concepts and perspective directions. Journal of Global Optimization (1993) Vol 3, Issue 4: pp 483-500.
[8] Krishnaswami, G.S. & Senapati, H. Reson (2019) 24: 87. https://doi.org/10.1007/s12045-019-0760-1
[9] J.S Haldane. Possible Worlds and Other Papers (1927), p. 286
[10] Strogatz, S.H. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton: CRC Press, 2019. Pp 10.
