A powerful logic, Boolean algebra is used for many things. Occum's net-net: DSRP can do Boolean, but Boolean can't do DSRP.
Boolean logic or algebra is predicated on three 'operators': OR, AND, and NOT. By combining these forms we can get a number of possibilities. In Boolean logic, all values are either True or False.
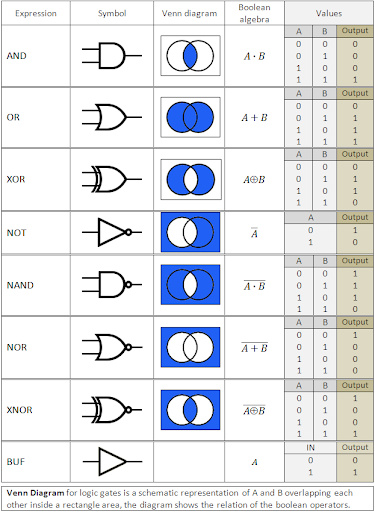
Boolean logic can be formed using [primarily] the D and R of DSRP. The D is for identity-other Distinctions. Identity-other (the elements) can be thought of as synonymous with is and is not. OR and AND are just types of action-reaction Relationships.
NOT-AND or NAND, for example, is simply the other or is not variable of Distinctions combined with the AND content-variable of Relationships. XNOR is merely the other to the XOR, and vice versa.
| XNOR | ||
| Input | Output | |
| A | B | A XNOR B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| XOR | ||
| Input | Output | |
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Thus, in XNOR, the system [A and B] is or is not. And, in XOR, either A is and B is not OR B is and A is not. Thus, it can be seen that S or part-whole Systems is utilized as well and of course Boolean logic itself is its own perspectival singularity. But the majority of the heavy lifting is being done by D and R.
So, Occum's net-net: DSRP can do Boolean, but Boolean can't do DSRP.
