Four is a number that shows up often, especially in fractals. DSRP is a fractal.
The idea of "fractured" dimensions can be traced back to the 1600s but was explored by Benoit Mandelbrot in 1967 [1] who cited Lewis Fry Richardson's previous research. Mandelbrot coined the terms "fractional dimensions" or "fractal" in 1975. The basic idea is that the smaller the ruler the longer the coastline; or more generally speaking, a change in scale results in a subsequent change in detail.
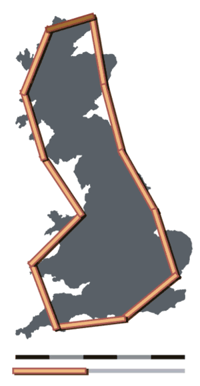
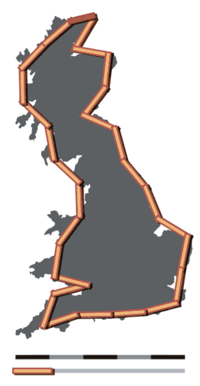

To understand fractal dimensionality one must distinguish it from 'normal' dimensionality (a.k.a., Euclidian) and also 'topical dimensionality' (a.k.a., Lebesgue) which although different are roughly similar in that:
| Entity | Dimension |
| point | 0 |
| line | 1 |
| plane | 2 |
| polyhedra | 3 |
| time | 4 |
The Koch snowflake (below) is a good example. Topologically it is 1 dimensional because it is a "line" yet the length between any two of its points is infinite. Therefore, no part of the Kock snowflake—no matter how small—is "line like" because it is made up of an infinite number of angled segments. Thus, its fractional dimensionality can be thought of as too simple to be 2-dimensional but too complex to be 1-dimensional. Its fractal dimension exists in between these two dimensions at ~1.262.
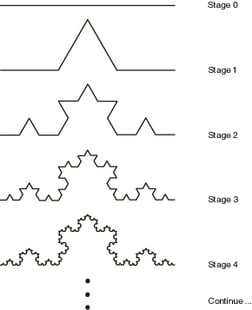

Carried out in 2 topical dimensions (a plane) the Koch snowflake looks and grows like this:

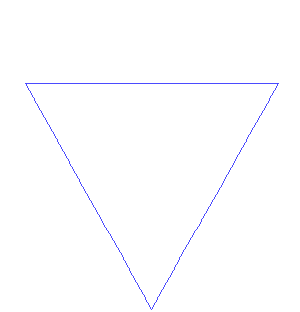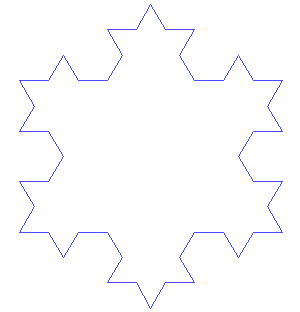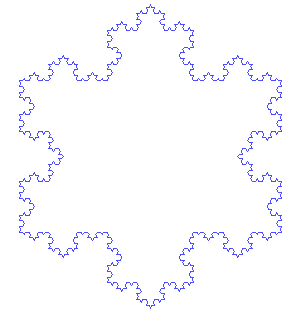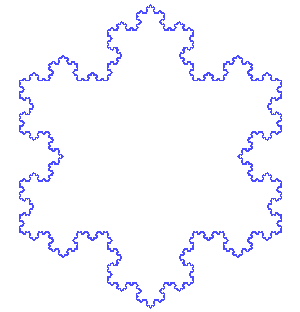
It exhibits self-similarity where any part is is exactly similar to the whole and where it is difficult to know at what level of scale on is at:

The fractal dimension, in this case, can range from 1.0 to 2.0. A low fractal dimension (1.1 or 1.2) may behave very much like a line. But a larger fractal dimension (1.9) has interesting properties in that as it fills the space of an area it acts as if it is filling the space of a volume.
The area increase with the square of the lengths (which holds true for any two dimensional shapes).
| Length | Area |
| 1 ft | 1 x 1 = 1 sq. ft. |
| 2 ft | 2 x 2 = 4 sq. ft. |
| 3 ft | 3 x 3 = 9 sq. ft. |
| 4 ft | 4 x 4 = 16 sq. ft. |
| 5 ft. | 5 x 5 = 25 sq. ft. |
| n ft. | n x n = n^2 sq. ft. |
The same is true for volumes. If we scale a factor of 2 (say 1ft to 2 ft) the volume of 1 cubic foot will increase to 8 cubic feet. The volume will increase with the cube of its linear dimensions.
| Factor | Volume |
| 2 | 2 x 2 x 2 = 8 cu. ft. |
| 3 | 3 x 3 x 3 = 27 cu. ft. |
| 4 | 4 x 4 x 4= 64 cu. ft. |
| 5 | 5 x 5 x 5= 125 cu. ft. |
| n | n x n x n= n^3 cu. ft. |
This means that when we scale volume we get significantly greater growth than when we scale area.
Now let's return to fractals or fractal dimensions. When fractal dimensions are higher (1.8, 1.9) the scaling effects act more like volume scaling than like area scaling. This means that we get more "space filling" due to the fractal structure. This additional dimension means that fractals fill and scale more like 3-dimensional volumes than they do 2-dimensional areas. Geoffrey West explains it this way,
A crinkly enough line that is space filling can scale as if it's an area. Its fractality effectively endows it with an additional dimension. Its conventional Euclidian dimension...still has the value 1, indicating that it's a line, but its fractal dimension is 2, indicating that it's maximally fractal and scaling as if it were an area. In similar fashion an area, if crinkly enough, can behave as if it's a volume, thereby gaining an effective extra dimension: its Euclidian dimension is 2, indicating it's an area, but its fractal dimension is 3.
DSRP is a fractal, self-similar repeating structure. It applies a simple ruleset across scale from the tiniest the the largest phenomena. If one thinks of an identity as a simple line segment, D, S, R, and P provide additional rules of transformation to that line segment, similar to the Koch snowflake thus space filling as if it was an area.

Figure: (1) If an identity (i) called ‘A’ exists (2) Then by definition an other (o) we can call ‘⌐A’ also exists (3) Therefore there is a relationship (R) between them. (4) In which an A-like action (A_a) has a ⌐A-like reaction (A_r) (5) And, vice versa, an ⌐A-like action (⌐A_a) has a A-like reaction (A_r) (6) Note that these action reaction variables are themselves identities (i). (7) A priori, when >1 identities are related, a system (S) exists in which all of the elements of the system are parts (p) (8) Ergo, a whole (w) must also exist. This whole we can call A/⌐A and it is also an identity (i). (9) An other (o) therefore exists, ad infinitum... (10) Note that the original system was defined entirely in terms of A. This means the frame of reference (perspective (P)) is A. But we could as easily have started with B, and defined the system in terms of B such that B is the point (ƥ) and ⌐B is the view (v). (11) Note that in this case A and ⌐A and B and ⌐B can simultaneously be identity (i), other (o), point (ƥ), or view (v) (12) In fact, all identities (i) can simultaneously be all of the element variables: identity (i), other (o), part (p), whole (w), action (a), reaction (r), point (ƥ), or view (v). Thus, all Patterns (DSRP) and all elements are simultaneous coupled oscillators that excite and inhibit
This is illustrated in the idea that four also comes from the fractal space filling and scaling laws. Where does the 'magical' number four come from? West [2] explains,
This additional dimension...leads to organisms' functioning as if they are operating in four dimensions. This is the geometric origin of the quarter power law. Thus, instead of scaling with classic 1/3 exponents, as would be the case if they were smooth nonfractal Euclidian objects, they scale with 1/4 exponents. Although living things occupy a three-dimensional space, their internal physiology and anatomy operate as if they were four-dimensional. (p.153)
In DSRP the number 4 also comes from what Cabrera calls 'mathematical enclosure' [3]—that 4 are needed for 1 and vice versa.
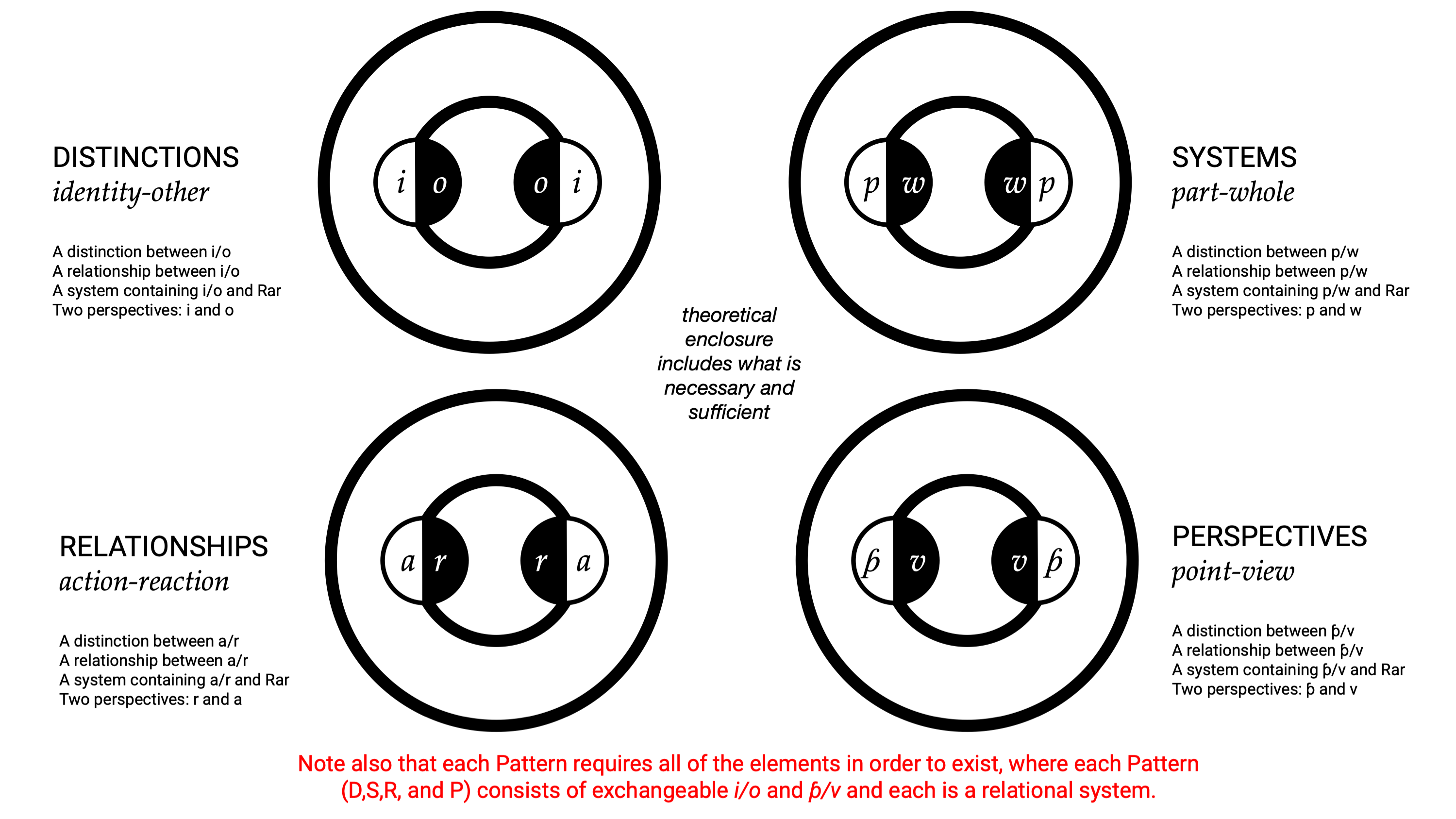
The fact that the whole of mathematics is built upon just four operators (+, -, x, and /), it stands to reason that these 'interaction rules' played out over 'oodles' of interactions would have some collective dynamics and emergent properties in the larger system of mathematics and human understanding. It is quite possible, although I am aware of no empirical studies or even conjecture on the matter, that the number 4 also arises as emergent from the basic interaction rules between the agents we call numbers.
References:
[1] Mandelbrot B. How long is the coast of britain? Statistical self-similarity and fractional dimension. Science. 1967;156: 636–638. doi:10.1126/science.156.3775.636
[2] West GB. Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies. Penguin; 2017. Available: https://play.google.com/store/books/details?id=Pf0jDwAAQBAJ
[3] Cabrera L, Cabrera D. Systems Thinking Made Simple: New Hope for Solving Wicked Problems. Ithaca, NY: Odyssean Press; 2015.
